【わかりやすく解説】帰無仮説・対立仮説・ｐ値・正規性検定とは【統計学】

統計学はとても役に立つツールですが、まぁとっつきにくいですね！今回は基礎の基礎、言葉の定義の確認です。自分用のメモでもあります。なるべく簡潔に書いたつもりです。

統計はバリバリ理系科目と思いきや、実は言葉の定義の理解が超重要です。計算は統計ソフトや簡単なものであればExcelを使えば一発でできますが、文章の理解は自分の力量にしか頼ることができません。

テキストの読解力が習得スピードを左右します。実は統計学を学んでいくにあたってまず重要なのは『専門用語の意味の理解』ですなんです。

この記事の概要

帰無仮説・対立仮説とは

帰無仮説および対立仮説とは『観測対象ＡとＢに差があるかどうかを検証する際の仮説』です。

帰無仮説：AはBと等しい
（A＝B）

対立仮説：AはBと等しくない
（A≠B）

例えばとある新薬を開発して効果の検証をしたいとします。

この新薬には血圧を下げる効果があるとします。複数人の被験者の血圧を新薬を飲む前と後で計測します。人によっては血圧に差が出る人と出ない人がいるとします。

さて、服用前と服用後で血圧に『差があるかどうか』を総合的に評価するのにはどうしたら良いでしょうか？

そんな時に使えるのが帰無仮説と対立仮説です。

服用前の血圧をAとしましょう。
服用後の血圧をBとしましょう。

帰無仮説を棄却できない場合（対立仮説を採択できない場合）は、服用前と服用後で差がない。
つまり、新薬の効果がないと評価できます。

A＝Bですね。

対立仮説を採択できる場合（帰無仮説を棄却できない場合）は、服用前と服用後に差がある。

つまり、新薬は血圧を下げる効果があると評価できます。

A≠Bですね。

p値が0.05以下であれば、帰無仮説を棄却することができます。
（帰無仮説が間違っているとみなすことができます。）

新薬の開発や改善活動では、AとBが等しくないことを望みますよね？だってせっかく時間と人員と予算を割いて開発したり変更したことが、何も手を加える前と同じ（A=B)ではやっている意味がありません。

なのでこう言ったケースでは、A≠Bを目指してプロジェクトが進みます。

つまり以下のように設定されることが多いです。

p値とは

p値とは『帰無仮説を棄却した時にそれが誤っている確率』です。

『ｐ値は調査結果が同じくらいになる確率』と言い換えることもできます。

0.05（５％）はめったに起こらないことの基準です。

なぜ5％なのかは、明確に公式などで説明することができません。

つまり、調査結果が同じくらいになる確率（P値）が0.05以下＝同じ手順で調査した際に同じ結果になる確率が５%以下＝差がある。と言えます。

または、データに差がないという仮説を棄却したときしたときに、それが誤りである確率（P値）が0.05以下＝差がある。と言えます。

帰無仮説が棄却されて対立仮説が採用されるというロジックです。

・基本的に棄却したい仮説を帰無仮説に設定します。
・検証したい内容を対立仮説に設定します。

結果としてｐ値が0.05以下だと帰無仮説が棄却されて、対立仮説が採用され、「差がある」と言えます。

ここまでが、帰無仮説・対立仮説・p値の説明です。

Pは「Probability」の略で「確率」Valueは「値」という意味です。

P値＝確率値です。そのままですね。

正規性検定について

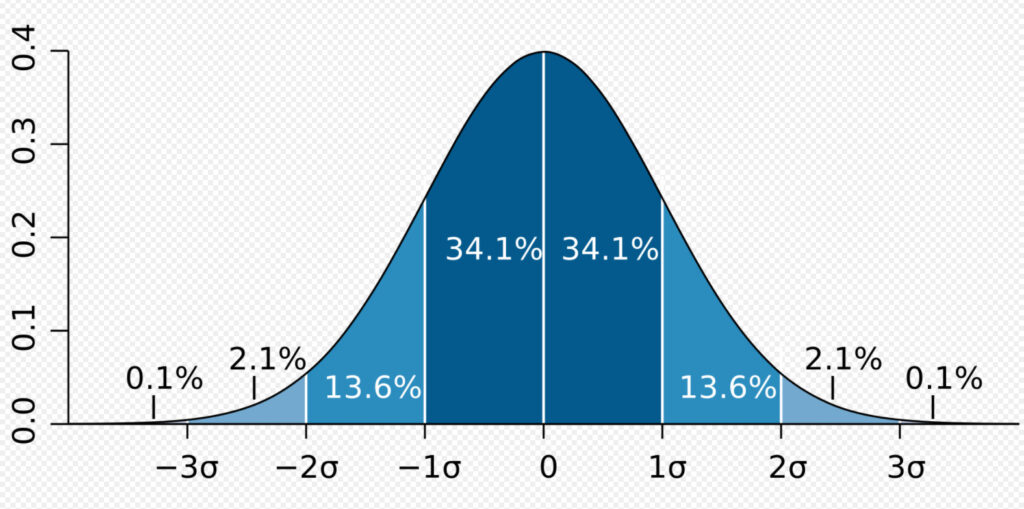
正規性検定とはデータの母集団が正規分布に従っているかどうかを調べるための検定です。

正規性分布に従っていないデータに、正規分布に従っている用のツールを使っても、統計的に正しい答えが求められません。ようはせっかく分析に統計的なアプローチを使っても得られる情報がデタラメになってしまうのです。

帰無仮説と対立仮説では以下のようになる傾向があると解説しました。

正規性検定の場合はデータの正規性を確認するための検定なので、『データは正規分布と等しい』ほうが嬉しいです。

帰無仮説：データの分布は正規分布と等しい（A＝B）
対立仮説：データの分布は正規分布と等しくない（A≠B）

つまり場合は、帰無仮説が棄却されないほうが好ましいのです。

正規性検定を実施するとｐ値が算出されます。

ｐ値が0.05以下だと帰無仮説が棄却されて、対立仮説が採用され、「差がある」ので、『データは正規分布と等しくない（A≠B）』になってしまいます。

だから正規性検定においてはデータは正規分布であるという結果になる、ｐ値が0.05より大きく『帰無仮説が棄却できない：データの分布は正規分布と等しい（A＝B）』という結果が望まれるのです。

正規性検定によってp値を算出するための難しい公式がありますが解き方について私は全く理解していません。笑

しかし統計ソフトを使えば一発で結果を求めることができるので実務で使う分には公式を理解する必要はないと考えています。

ソフト：Minitab
手順A：統計→基本統計→正規性検定→データ入力→OK→p値確認
手順B：統計→基本統計→記述統計グラフ要約→データ入力→OK→p値確認
※手順はABどちらでもOKです。