『標準偏差』が分かればバッチリ数値で評価することができます。
数値を評価するときに『平均』だけ見ていませんか?
例えば平均点が60点のテストで70点だったら直感的に良い結果だと思うのではないのでしょうか?
しかし、本当に良い結果だったかどうかは『標準偏差』による『データのバラツキ』まで考慮しないと判断できないのです。
今回は統計学の圧倒的スター!『標準偏差』を解説します!
私は、標準偏差の理解は統計を学ぶ上で最初に立ちはだかるハードルだと考えています。
なぜなら統計とは確率の学問であり、確率を求めるにはデータのバラツキを知ることが必要であり
バラツキこそが標準偏差だからです。
そしてこの『標準偏差』ですがひとたび理解するとものすごく役に立ちます!
学力を数値化する『偏差値』も『標準偏差』から計算されています。
平均点という『ポイント』だけの観点ではなく、『標準偏差』が理解できれば、データ全体の『ばらつき具合』が分かるようになります。
僕には3歳になるかわいい子供がいます。
こどもが、小学校にあがり、テストの点数で評価されるようになる前に『標準偏差』をしっかり学ぶ機会があって本当に良かったと思っています。
なぜなら、ほとんどの人はテストの点数評価に『平均値』しか考慮せず、データ全体の『ばらつき』を考えもしないからです。
子供が取ってきた点数が『平均』より上だったか下だったか。実はこれ、標準偏差を考慮すると、どのくらい平均から離れているかということも重要になります。
学校だけでなく、世の中なんだかんだ数字で回っています。

それではさっそく便利で楽しい『標準偏差』を学んでいきましょう!
標準偏差とは
『各データの値と平均差の2乗の合計を、データの総数nで割った値の正の平方根』です。
一般的には観測したデータの全体の『バラツキ』を示す値です。
・
・
・
・
・
は?
と、思うのも無理はありません。
私も初めて標準偏差とは何かを理解しようとしたときに、「あ、無理だこれ」と思いました。
でも大丈夫です!順を追って理解していけば絶対に理解できます!
偏差=バラツキです。全体のバラツキを表すため『標準偏差』という名称がついています。
ちなみに英語ではStandard deviationと言います。
Standard(標準的な)deviation(偏差=偏り=バラツキ)です。そのままですね。
標準偏差は2種類ある
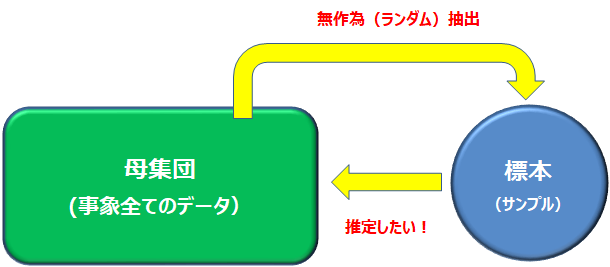
標準偏差とは記号 σ または s で表わされる値です。
σ で表すときは母集団の標準偏差、s で表すときは標本の標準偏差を指すことが多いです。
● σ:母集団の例「日本人1億人全体」
● s:標本の例「アンケートに参加した3000人」
データが母集団全てなのかそれともランダム抽出した標本なのかによってσかsなのかが変わります。
σとsの違い
母集団(事象全てのデータ)から算出されるのがσです。ちなみに『シグマ』と読みます。
母集団(事象全てのデータ)から標本(サンプル)を取り出してそのデータをもとに算出されるのがsです。
調べたけどsのほうは読み方不明です。
(私はサンプルの標準偏差と言っています)
1標準偏差はどのくらいのバラツキか?
事象はバラツキます。
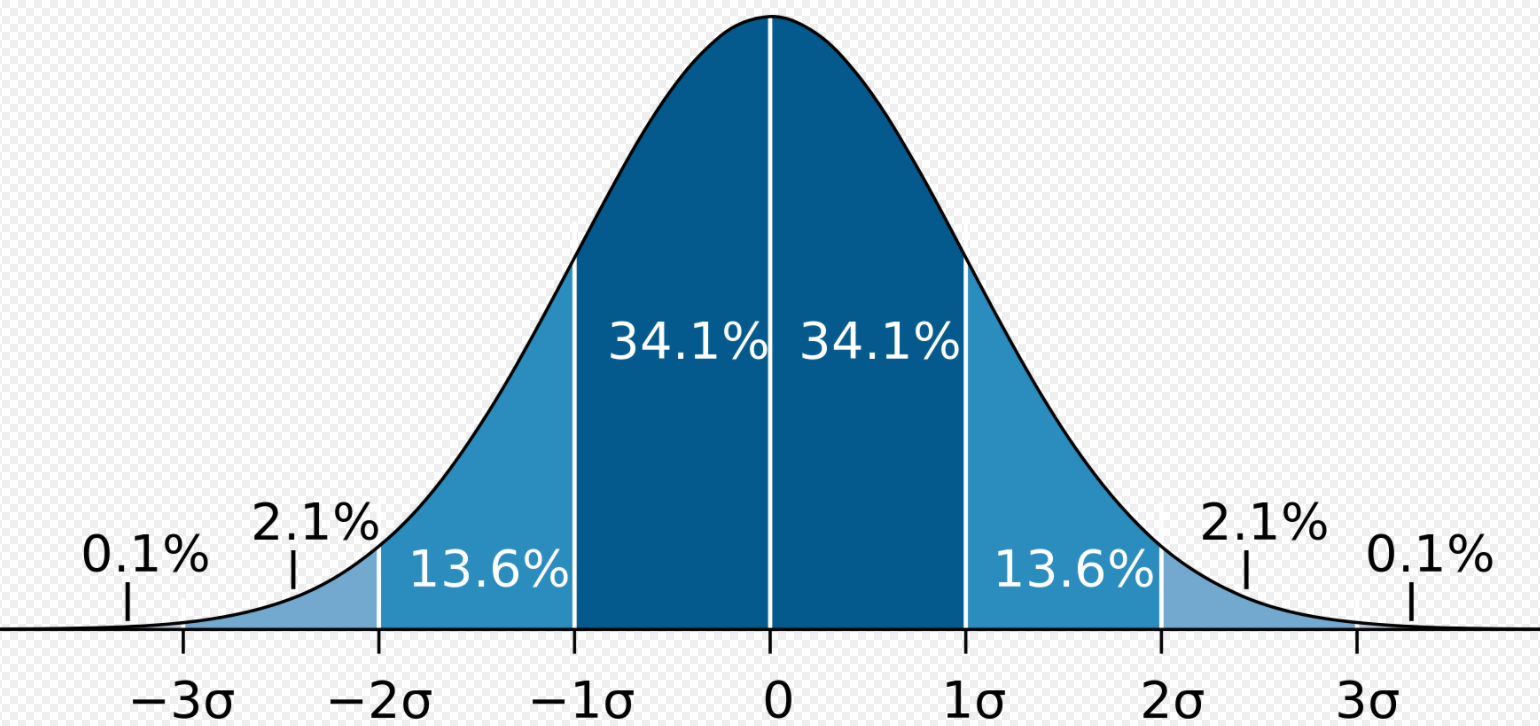
下の図は、高さが頻度で左右がバラツキを示しています。
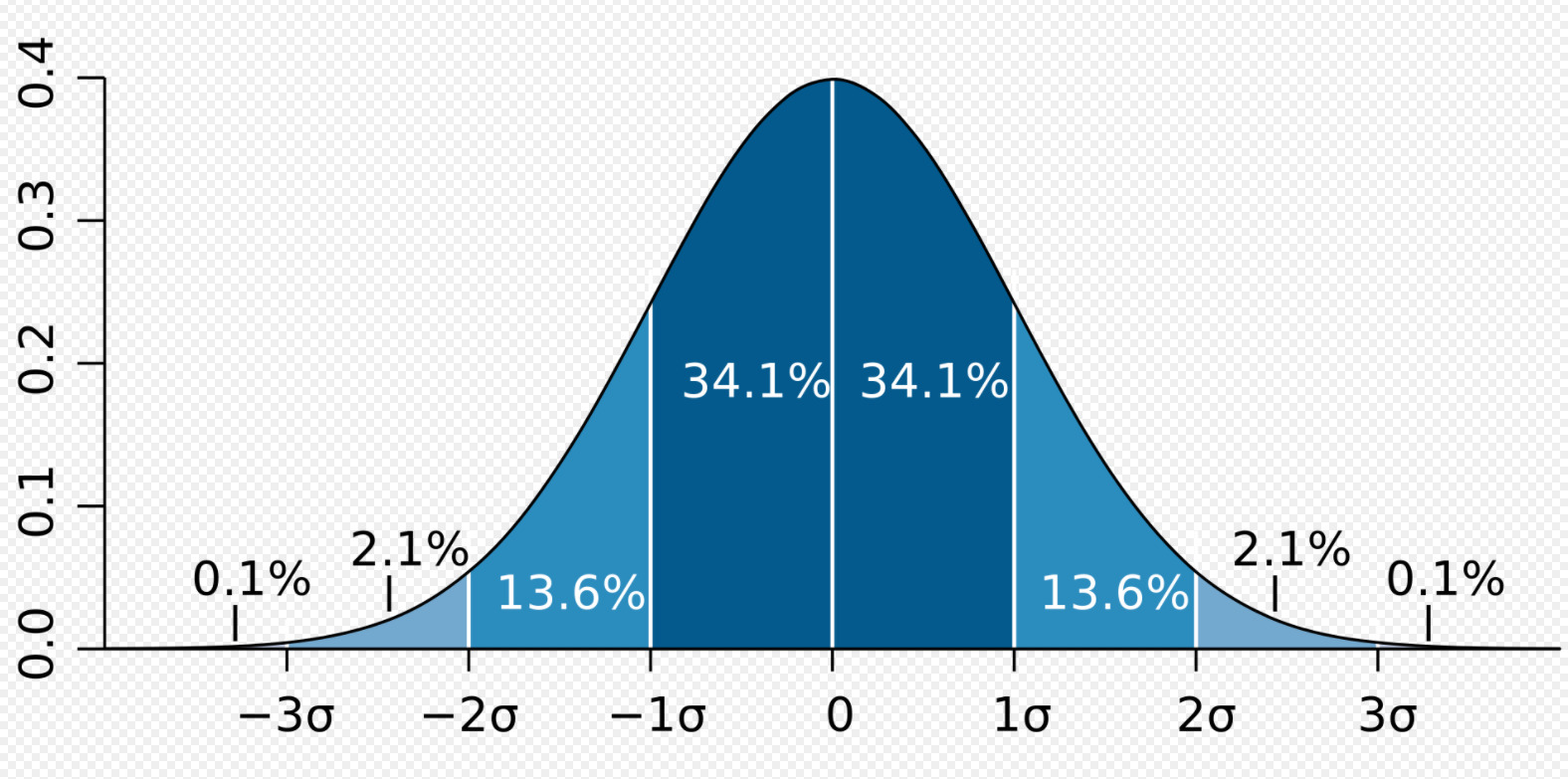
引用:Wikipedia
中央に近ければ近いほど狙った通りの結果に近く、遠いものは狙った結果と差異が大きいことを示しています。
製造現場でいえば、中央を狙って製造される製品は、もちろん中央の値に生産されることが一番多いです。
しかし結果はいろいろな要因の影響を受けてバラツキます。
生産者は常にターゲット(上のグラフでいうところの0)を狙っているので、中央の頻度が一番多く末広がりに頻度が少なくなります。
全ての事象が100%(図のグラフの面積全て)だとすると、1標準偏差は34.1%になります。
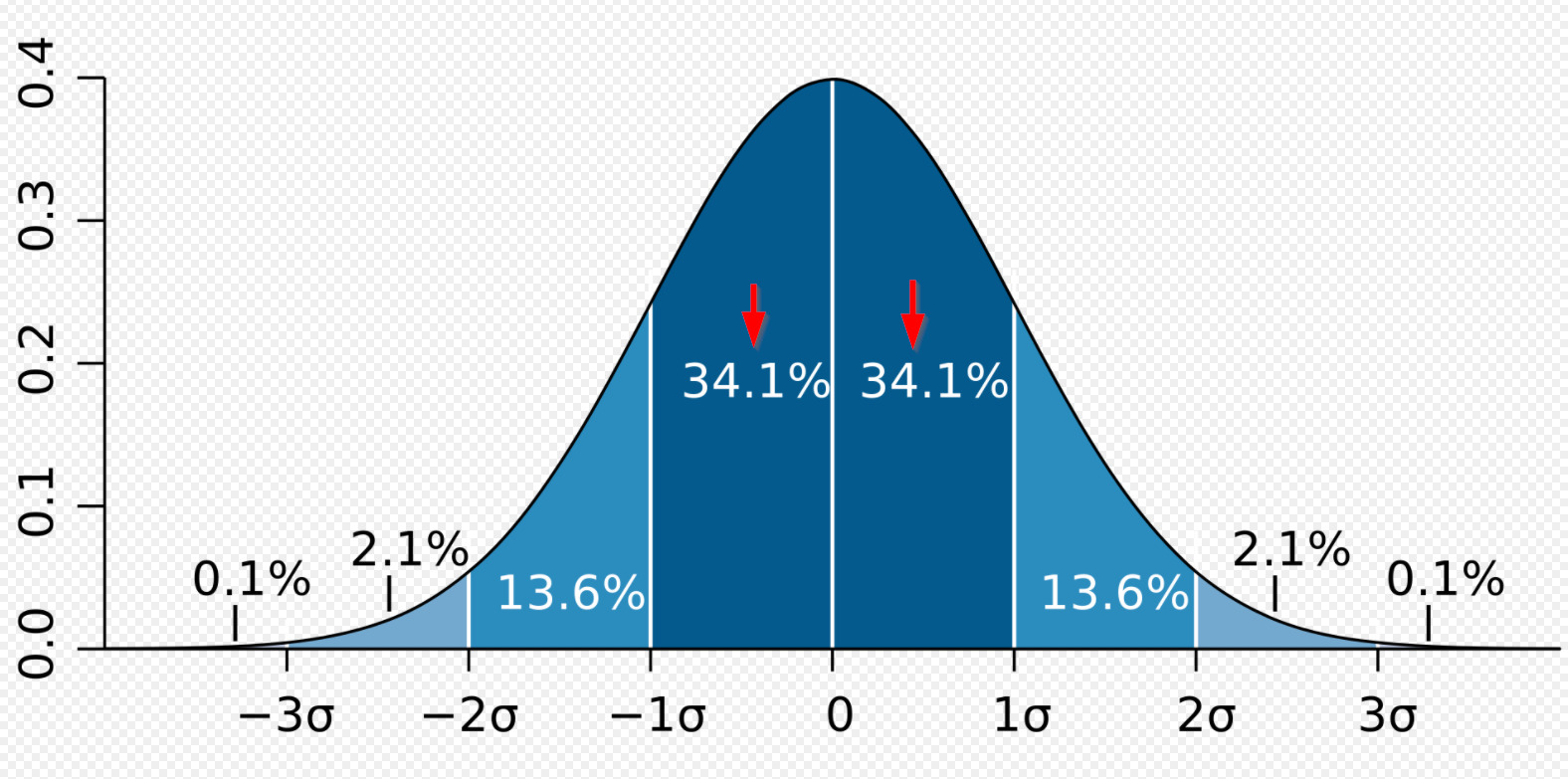
プラスマイナス1標準偏差で68.27%となり。約7割の事象が含まれることになります。
言い換えれば、プラスマイナス1標準偏差内であれば、観測した事象に対して約7割の確率で起こり得ることだと評価できます。
ちなみにプラスマイナス2標準偏差で95.47%、プラスマイナス3標準偏差では99.6%になります。
バラツキを具体的にイメージしてみよう
ダーツで10回投げた時の結果を例にとって考えてみましょう。
ダーツの専門的なルールは置いておいて、プレーヤーはとにかく中央を狙って投げることを想定します。
10投入とも中央に集中している場合プレーヤーは狙った場所に投げることができていと言えます。
つまりバラツキが小さいといえます。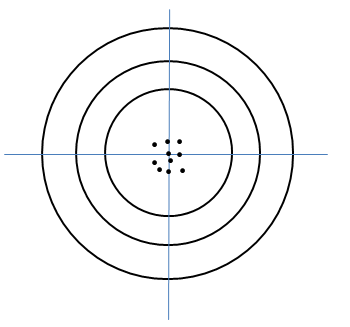
10投入が上も下も右も左もばらばらにばらけてしまっているとします。
これはばらつきが大きいといえます。
標準偏差と偏差値
面白いことに、学校のテストのように全員が100点を目指している(ことになっている)事象に対しても、この正規分布が当てはまります。
この現象をさらに感覚的にわかりやすく変換したのが『偏差値』です。
割愛しますが、ある公式によって、分布の中央である『0』の値を『50』に変換します。
標準偏差は自分の点数だけでなく、全体のバラツキから算出されます。
つまり標準偏差を変換させた偏差値も、全体のバラツキから算出されます。
全体のバラツキから算出されることによって、自身のスコアだけでなく、全体のバラツキを基準に、自分が全体のどの位置にいるのかを把握することができます。
例えば受験者が15人いるテストで90点を取った場合、自身のスコアが全体の平均に対して非常に高いような場合は以下のような偏差値になります。
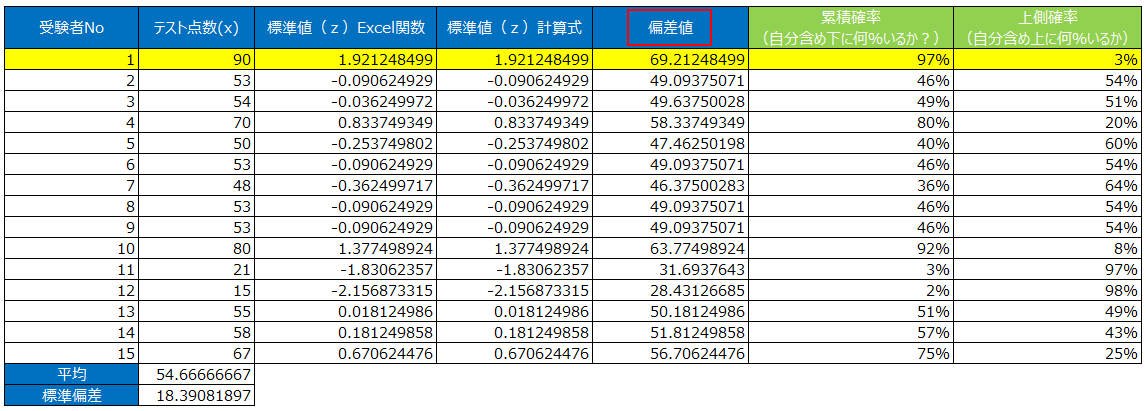
受験者No1の人は90点を取ったので、偏差値69.21と50よりも高く、自分より上に3%の受験者しかいないので非常に成績が良いと評価できます。
※15人中1番点数が良いのに、自分より上に3%いるという意味は、今回の15人だけでなく、そこから『全体』を推定した場合の確率になります。
ちなみにテストの結果が以下ような場合、受験者No1の人はたとえ90点を取っていたとしても偏差値43.44と50よりも低く、自分より上に74%の受験者がいるので成績が悪かったという評価になります。
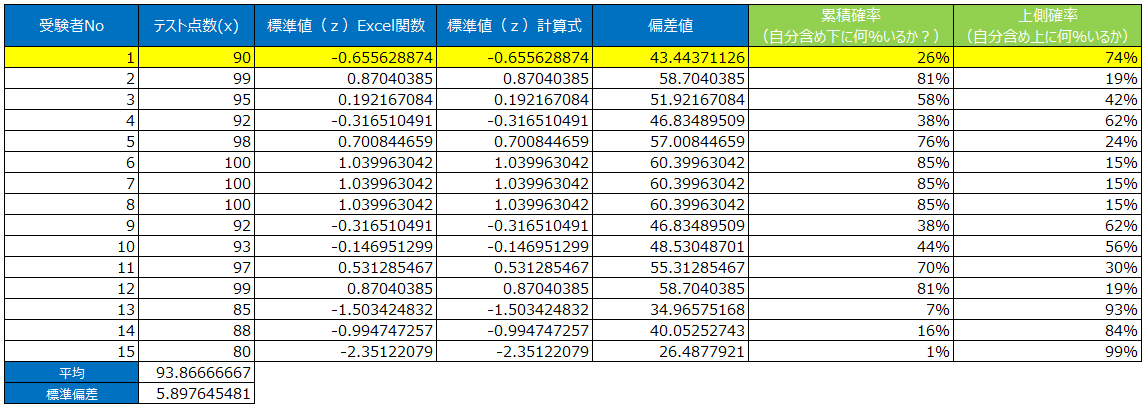
『標準偏差』から『偏差値』に話がそれてしまいましたが、『バラツキ』を使うことの利点が分かってきたのではないでしょうか?
公式を見てみよう
それではどのように標準偏差を算出するのか、公式を見てみましょう。
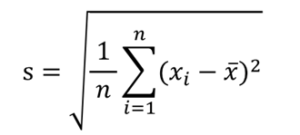
・
・
・
・
・
は?
そうですね!2回目の『は?』ですよね!
果たして自分にはこんな公式を使って計算ができるのかと思われた方もいるかと思いますが、大丈夫です。ひとつずつ理解していきましょう。
私ですら理解できたんだから、あなたにも必ず理解できるはずです!
ちなみにExcelの関数を使えば一発で計算できるので後で紹介します。
【公式のつまづきポイント解説※最初は読み飛ばしてもOKです】
なぜ√が必要なのか?(なぜ平方根をとるのか?)
標準偏差を求めるにはまず『分散』を求める必要があります。
標準偏差の2乗=分散なので、つまり分散の平方根=標準偏差となります。
なぜ標準偏差の2乗が分散なのか?
そもそも標準偏差を求めるためには分散を計算しなければいけません。
計算の工程で全てのサンプルに対して、平均値からの差を計算して2乗してます。
2乗されたそれぞれの値の和をサンプルの数で割ると分散が求められます。
2乗する理由は、平均値よりも低い値がマイナス値となり、そのままでは総和の計算結果が0になってしまうためです。
全ての『差』に対して2乗すれば、マイナスの値も全て正の値になります。
全て正の値に変換して計算しているため、標準偏差は正の値に対するバラツキしか表現できません。
そのため、平均値からどの程度ばらついているかを表す際に±1と考える必要があります。
式は複雑ですが『標準偏差=バラツキの大きさ』と理解していればOKです。
公式を分解して解説
この公式によってデータは以下のように処理されていきます。
①各計測値から全体の平均を引いたものを2乗する。
(マイナスの算出結果をプラスに変換している)
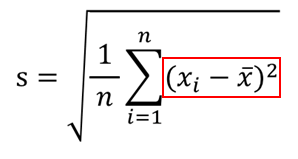
②それらを全て足し合わせる
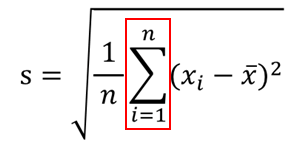
③それらをデータの数で割る(平均を取る)
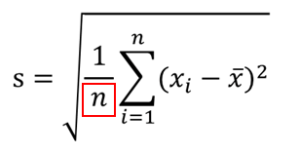
④さら平方根を取る(単位を元に戻す)
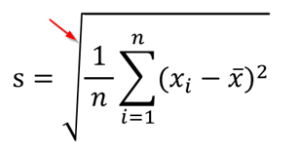
ということをしています。
一つずつ説明していきます。
①各計測値から全体の平均を引いたものを2乗する
これは、各観測値と平均値の差を『面積』であらわすためのプロセスです。
仮に観測値が5cmで平均値が0cmだとしましょう。
観測値と平均値の差は5cm-0cmで5cmですね。
バラツキを知りたいのであればこれでいいじゃんと思うかもしれませんが、都合の悪いケースがあります。
そう、差がマイナスになる場合です。
データ全体のバラツキを確認したいので、観測値-平均値を計算すると、計算結果がマイナスになる場合が必ずあります。
各観測値から平均値を引いたものを全て足すと、必ず0になってしまうのです!
観測値が-5cmだった場合は、観測値と平均の差は-5cm-0cmで-5cmになります。
5cm-5cmは0ですね。0をどんな数字で割っても計算結果は0です。
データは確かに+5cmと-5cmのようにプラスにもマイナスにもばらついているのに、バラツキ=標準偏差は0という結果になってしまいます。
平均との差異を線で表す場合(単位:cm)
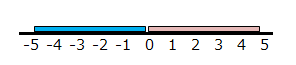
このジレンマを解消するために、2乗のプロセスが必要になるのです。
②それらを全て足し合わせる
マイナスの値は2乗してやればプラスになります。
ただし2乗することで情報は線から面に変わります。(単位:cm2)
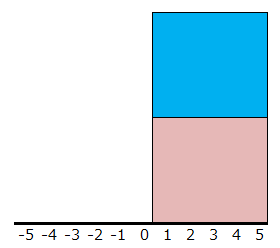
さらにこれを正方形としてとらえます。(単位:cm2)
(面積は5×5×2なので50。一辺の長さ(50の平方根)が7.071・・・の正方形になる)
③それらをデータの数で割る(平均を取る)
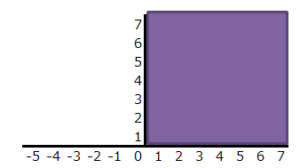
この面積は各観測値と平均の差の二乗の和なので、バラツキの平均ではないです。
平均にするために観測値の個数で割ります。(50÷2=25)
25の平方根は5なので一辺の長が5の正方形になります。
これが『面で見た場合のバラツキ』である『分散』です。(単位:cm2)
④さら平方根を取る(単位を元に戻す)
このままでは『面で見た場合のバラツキ』なので、各観測値のバラツキを示すにはもともとの単位と異なり都合が悪いです。
今回の観測データの単位がcmなのに、このままでは単位がcm2のままです。
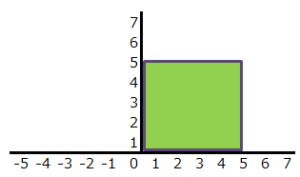
平方根を取ることによって、面積から線の情報に変換します。(cm2からcmに変換)
25の平方根は5なので、今回のバラツキは5cmという計算結果になります。
これが『線で見た場合のバラツキ』である『標準偏差』です。(単位:5cm)
![]()
このままではプラス側の標準偏差しか表現できていません。
マイナス側も考慮するために、最終的に標準偏差は『±5』と表記されます。
Excelの関数を使って算出する方法
Excelの関数で簡単に標準偏差を算出できます。
データが母集団の場合はStdev.pを、標本の場合はStdev.sを使いましょう。
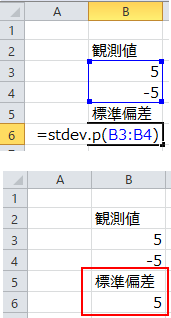
標準偏差の単位
よくある質問で、「標準偏差の単位は?」というものがあります。
ここまでの説明を読んでいただければわかるように、標準偏差の単位は観測されたデータの値に依存します。
・cmでデータが計測されれば標準偏差の単位はcmです。
・kgでデータが計測されれば標準偏差の単位はkgです。
ちなみに、異なる単位のデータをひとまとめにして標準偏差を算出することはできません。
『標準偏差』が何なのか分かったところで、じゃあどんなことに役立つの?という疑問が浮かぶと思います。
テストの点数と評価について考えてみましょう。
平均点が60点のテストで70点を取るのはどのくらいスゴイ事?
多くの方が「平均を超えているならそこそこ凄いんだろうな~」といった感想を持つはずです。
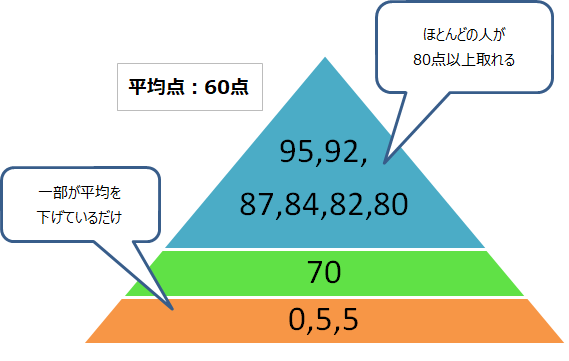
しかし、もしそのテストの点数分布が「0点、5点、5点、70点、80点、82点、84点、87点、92点、95点」(平均点60点)だとしたらどうでしょう?
標準偏差を算出するために公式に当てはめる場合、以下の関係が成り立ちます。

Excelで計算してみました。
点数
0
5
5
70
80
82
84
87
92
95
標準偏差
37.67
60点±37.67点がバラツキです。
22.33点から97.67点までの範囲が標準偏差内となります。
つまり70点を取っても特にすごくはないことが分かります。
「ごく一部の生徒の点数が極端に低く、それが原因で平均が下がっただけで、普通に勉強したら80点以上取れるテストだった」と評価できます。
なんなら、一番点数の良かった95点ですら、97.67点以下なので、『誤差の範囲内』と評価することができます。
このようなテストでの70点はやや努力不足かもしれません。上位集団の中では一番点数が低いです、少なくともスゴイ事とは言えません。
では、もしそのテストの点数分布が「45点、50点、53点、60点、60点、60点、62点、65点、70点、75点」(平均点60点)だとしたらどうでしょう?

こちらもExcelで標準偏差を計算します。
点数
45
50
53
60
60
60
62
65
70
75
標準偏差
8.53
60点±8.53点がバラツキです。
51.47点から68.53点の範囲が標準偏差内となります。
つまり70点はバラツキ以上の点数をとれているので優秀と評価できます。
今回のケースですと70点はクラスで2位の成績です。
点数分布から『多くのほとんどの生徒が間違えた難問を正解することができた』とも推測できます。
このように、平均という数字は情報量が少なく、それだけでは意外と役に立たない数字なのです。
そこで役に立つのが「バラツキの大きさを表す数値」である標準偏差なんでんすね。
テストを平均点と標準偏差という2つの視点からみることで、「70点を取ったこと」がどのくらいスゴイ事なのかが一気に分かりやすくなるんです。
一般的なテストの標準偏差が10~25点なのだそうです。
テスト点数の標準偏差を確認することで、その人の取った点数がスゴイのかスゴくないのかを、全体のバラツキ込みで評価することができます。
ここまで読んでいただけたのであれば、テストの点数を『平均点』と比べただけでは十分に評価できないことがお分かりいただけたと思います。
これから先、何かを点数で評価するときには、ぜひ『標準偏差』を思い出してみてください。















コメント