
年収や身長や体重・・・。人生にはいろんな数字がついてまわります。そして気になるところはやはり『自分は一般的な基準と比べてどうなんだろうか?』という点ではないでしょうか。
そんな時に真っ先に思い浮かぶのが【平均値】ではないかと思います。しかし、世の中のいろんな数字を【平均値】だけで判断しても、時として自分がほしい情報を正確に得られないかもしれません。
今回は、実は【平均値】よりも大切かもしれない【中央値】の解説です。
この記事の概要
・平均値と中央値の特徴
・エクセルで中央値を計算する方法
中央値とは
中央値とはデータを小さい順に並べた時の真ん中の値です。

奇数だといい感じに真ん中のデータを特定できますが、偶数だと真ん中のデータというのは存在しません。そんな時は、真ん中二つのデータの平均値が中央値になります。

なぜ平均値では不十分で中央値を考える必要があるのか具体例でみていきましょう。
同窓会に出席したとします。出席者はあなたを含めて11人です。この11人の年収を全て把握できたとします。
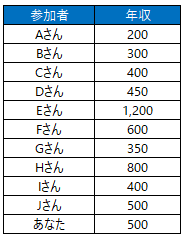
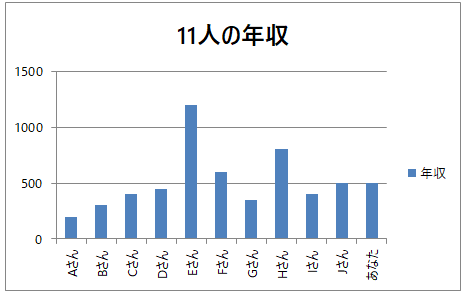
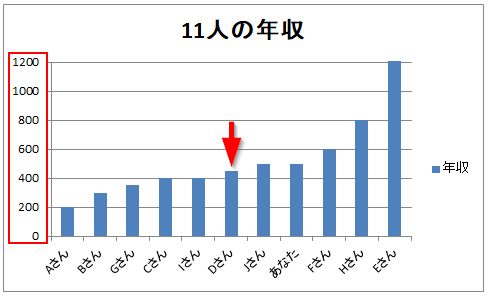
一番年収が低い人で200万円、高い人は1,200万円でした。あなたの年収は500万円です。
この11人の平均年収は約520万円です。あなたの年収500万円は平均と比べると低いという評価になります。
11人を年収の低い順に並べて中央値を確認してみましょう。平均値は合計をデータの数で割った値ですが、中央値の場合は小さい順に並べた際のど真ん中の値を採用します。
そうなると中央値は下から数えて6番目のDさんの450万円になります。
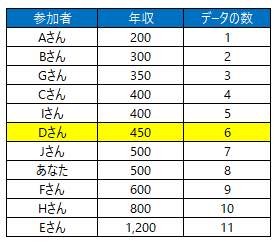
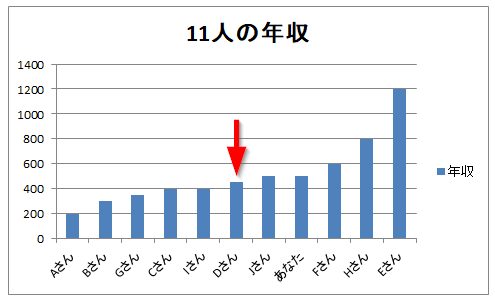
中央値450万円に対してあなたの年収は500万円なので上回っています。
さて、平均値と中央値ではあなたの年収の評価が変わってしまいました。
どちらの評価が適切なのでしょうか?

正解は、あなたの年収500万円は中央値の450万円に対して高い。という評価です。
この場合だとあなたの年収は平均値に対して低いという評価は決して正しいとは言えません。
なぜでしょうか?
それは、平均値は外れ値に影響を受けやすく、中央値は外れ値の影響を受けにくい特徴があるからです。
同窓会に集まった11人の例をもう一度使って考えてみます。
ただし、今回は先ほどのケースでは年収1,200万円としていたEさんの年収を1億円にしてみましょう。
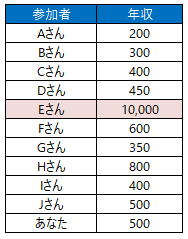
集まった11人のなかで年収1億円というのはあきらかにデータの傾向から大きく逸脱した外れ値です。
11人の平均年収は約1,320万円になってしまいます。
これでは平均を超える年収を得ているのはEさんだけになってしまいます。
平均とはなんだったのでしょうか・・・。いや、これこそが【平均値】の実態なんです。
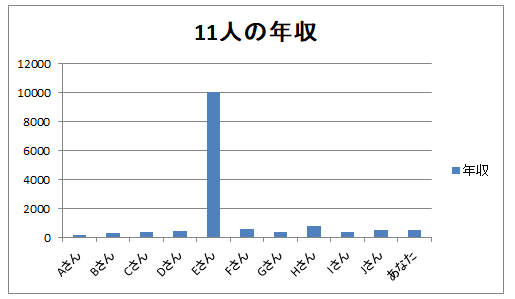
グラフにすると一目瞭然です。年収1億円という「異物」が混入したことでその他10人の棒グラフはほとんど見分けがつかないくらい小さく表示されるようになってしまいました。
Eさんからしたら年収に関しては他の10人はドングリの背比べにしか見えないでしょう。ほかの10人からしたらEさんは特別だから年収の比較対象としてはひとくくりにしてほしくはないでしょう。
幼稚園の運動会にプロのアスリートがまぎれ込んでいるようなものです。
それでは気を取り直して【中央値】を考えてみましょう。
年収1億円という「異物」が入ろうが、中央値は変わりません。値の小さい順に並べて、値の個数の真ん中のデータが中央値だからです。Eさんの1億円という外れ値が入ってきても、中央値は変わらずに450万円です。
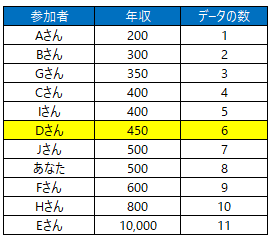
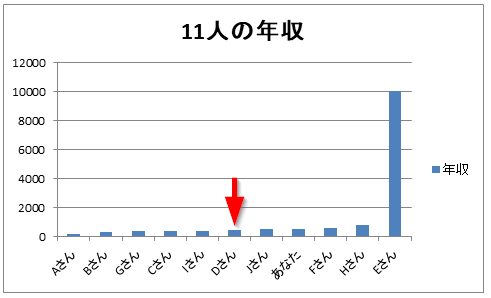
グラフの上限を1,200万円に制限して見やすくしてみました。(Eさんのグラフは見えていないだけで枠を突き抜けてはるか上まで伸びています)
さて、たったひとりの1億円プレーヤーが現れたことで平均値は1,320万円まで跳ね上がりました。あなたの年収500万円は平均値と比べてダブルスコアで低いです。しかし、中央値は変わらず450万円です。

ここまで読んでいただければ、自分の年収を評価する時には平均値ではなく中央値を参考にしたほうが良いということがご理解いただけたのではないかと思います。
年収だけではなく、身長だって、体重だって、参考にするデータの中に外れ値が混ざれば混ざるほど、平均値は外れ値の影響を受けます。
平均値と中央値の特徴
平均値は全体の傾向をつかみやすいのが特徴
11人の同窓会メンバーの中で1億円という年収は圧倒的に外れ値ですが、年収1億円の人がいるという事実は変わりません。年収1億円の人がいるという事実を踏まえたうえで11人の年収の『傾向』を把握するには平均値を参考にすることが適しています。
中央値は外れ値に影響されにくいのが特徴
11人の同窓会メンバーの中で1億円という年収はどう考えても外れ値です。『一般的な』基準に対して自分が上か下かを考える時に、イレギュラーな要因は極力とりのぞきたいところです。そんなときに使えるのが中央値です。
Excelで中央値を求める方法
中央値を求める関数は[MEDIAN]です。

ちなみにエクセルではデータタブからデータ分析と進み基本統計量を使えば、平均値、中央値の他にも基本的な統計データを一発で表示することができます。
大きいデータをポンと渡されたときに、まずは基本統計量をパッと出してみてデータの全体像をつかみたいときにとても役立ちます。
今回使った11人の年収データを使って基本統計量を表示させるとこんな感じになります。

見慣れない項目が多いと感じる人にはちょっと難しく感じるかもしれませんが、平均にくわえて今回紹介した中央値もバッチリ表示されているのが分かるかと思います。
さらに、最頻値や、範囲、最小、最大、合計、標本(データの個数)あたりは名称だけでも直感的に理解できるのではないでしょうか。これらのパラメーターが一発で表示できるのでとても便利な機能で重宝してます。
『統計』と聞くと、ウッと苦手意識を感じる方もいるかもしれません。私もそうでした。
けど、なにも難しい公式を理解して超難しい問題を解決するためのデータをはじき出すことだけが『統計』ではありません。
今回解説した中央値をはじめとする、平均値や最大値や最小値やそのたもろもろのデータの特徴を要約した数値は、統計量と呼ばれます。
統計のなかでも基本中の基本を押さえておくだけで、いろんな情報に触れた時に多角的に物事を見ることができるようになります。
そんな統計の、基本中の基本を、ひたすらやさしくかみ砕いて説明してくれている本を紹介します。













コメント